Полный факторный эксперимент
Как выбрать локальную область факторного пространства, где ее выбирать и какого размера она должна быть? Это важный этап принятия неформализованных решений, предшествующих построению плана первой серии эксперимента.
Весь процесс исследования можно считать состоящим из последовательности этапов, часть из которых полностью формализованы, а часть требуют «интуитивных» решений. Причем, по мере развития теории, формальные этапы будут играть все большую роль, но до конца не вытеснят неформализованные этапы.
Принятие решений перед планированием эксперимента
При выборе области эксперимента должны учитываться следующие соображения.
Прежде всего, надо оценить границы областей определения факторов. При этом должны учитываться ограничения нескольких типов. Первый тип: принципиальные ограничения для значений факторов, которые не могут быть нарушены ни при каких обстоятельствах. Например, если фактор – температура, то нижним пределом будет абсолютный нуль. Второй тип – ограничения, связанные с технико-экономическими соображениями, например, со стоимостью сырья, дефицитностью отдельных компонентов, временем ведения процесса. Третий тип ограничений, с которым чаще всего приходится иметь дело, определяется конкретными условиями проведения процесса, например, существующей аппаратурой, технологией, организацией. В реакторе, изготовленном из некоторого материала, температуру нельзя поднять выше температуры плавления этого материала или выше рабочей температуры данного катализатора.
Оптимизация обычно начинается в условиях, когда объект уже подвергался некоторым исследованиям. Информацию, содержащуюся в результатах предыдущих исследований, будем называть априорной (т.е. полученной до начала эксперимента). Мы можем использовать априорную информацию для получения представления о параметре оптимизации, о факторах, о наилучших условиях ведения процесса и характере поверхности отклика, т.е. о том, как сильно меняется параметр оптимизации при небольших изменениях значений факторов, а также о кривизне поверхности. Для этого можно использовать графики (или таблицы) однофакторных экспериментов, осуществлявшихся в предыдущих исследованиях или описанных в литературе. Если однофакторную зависимость нельзя представить линейным уравнением (в рассматриваемой области), то в многомерном случае, несомненно, будет существенная кривизна. Обратное утверждение, к сожалению, не очевидно.
Итак, выбор экспериментальной области факторного пространства связан с тщательным анализом априорной информации.
Выбор основного уровня
Наилучшим условиям, определенным из анализа априорной информации, соответствует комбинация (или несколько комбинаций) уровней факторов. Каждая комбинация является многомерной точкой в факторном пространстве. Ее можно рассматривать как исходную точку для построения плана эксперимента. Назовем ее основным (нулевым) уровнем. Построение плана эксперимента сводится к выбору экспериментальных точек, симметричных относительно нулевого уровня.
В разных случаях мы располагаем различными сведениями об области наилучших условий. Если имеются сведения о координатах одной наилучшей точки и нет информации о границах определения факторов, то остается рассматривать эту точку в качестве основного уровня. Аналогичное решение принимается, если границы известны и наилучшие условия лежат внутри области.
Положение усложняется, если эта точка лежит на границе (или весьма близко к границе) области. Тогда приходится основной уровень выбирать с некоторым сдвигом от наилучших условий.
Может случиться, что координаты наилучшей точки неизвестны, но есть сведения о некоторой подобласти, в которой процесс идет достаточно хорошо. Тогда основной уровень выбирается либо в центре, либо в случайной точке этой подобласти. Сведения о подобласти можно получить, анализируя изученные ранее подобные процессы, из теоретических соображений или из предыдущего эксперимента.
Наконец, возможен случай с несколькими эквивалентными точками, координаты которых различны. Когда отсутствуют дополнительные данные (технологического, экономического характера и т.д.), выбор произволен. Конечно, если эксперимент недорог и требует немного времени, можно приступить к построению планов экспериментов вокруг нескольких точек.
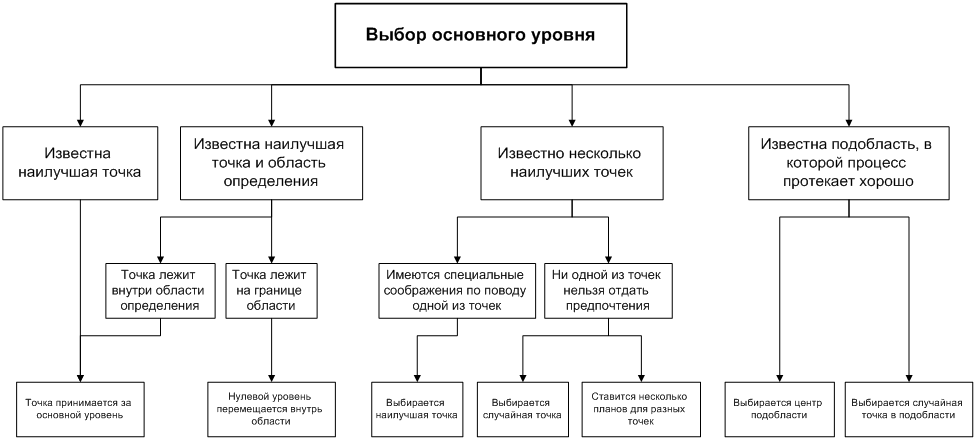
Резюмируем наши рассуждения о принятии решений при выборе основного уровня в виде блок-схемы
Рисунок 2
После того как нулевой уровень выбран, переходим к следующему шагу – выбору интервалов варьирования.
Выбор интервалов варьирования.
Теперь наша цель состоит в том, чтобы для каждого фактора выбрать два уровня, на которых он будет варьироваться в эксперименте.
Интервалом варьирования факторов называется некоторое число (свое для каждого фактора), прибавление которого к основному уровню дает верхний, а вычитание – нижний уровни фактора. Другими словами, интервал варьирования – это расстояние на координатной оси между основным и верхним (или нижним) уровнем. Таким образом, задача выбора уровней сводится к более простой задаче выбора интервала варьирования.
Заметим еще, что для упрощения записи условий эксперимента и обработки экспериментальных данных масштабы по осям выбираются так, чтобы верхний уровень соответствовал +1, нижний –1, а основной – нулю. Для факторов с непрерывной областью определения это всегда можно сделать с помощью преобразования
![]() ,
,
где
![]() – кодированное
значение фактора;
– кодированное
значение фактора;
![]() – натуральное значение фактора;
– натуральное значение фактора;
![]() – натуральное значение основного уровня;
– натуральное значение основного уровня;
![]() – интервал варьирования;
– интервал варьирования;
![]() – номер фактора.
– номер фактора.
Для качественных факторов, имеющих два уровня, один уровень обозначается +1, а другой –1; порядок уровней не имеет значения.
На выбор интервалов варьирования накладываются естественные ограничения сверху и снизу. Интервал варьирования не может быть меньше той ошибки, с которой экспериментатор фиксирует уровень фактора. Иначе верхний и нижний уровни окажутся неразличимыми. С другой стороны, интервал не может быть настолько большим, чтобы верхний или нижний уровни оказались за пределами области определения. Внутри этих ограничений обычно еще остается значительная неопределенность выбора, которая устраняется с помощью интуитивных решений.
Обратите внимание, что при решении задачи оптимизации мы стремимся выбрать для первой серии экспериментов такую подобласть, которая давала бы возможность для шагового движения к оптимуму. В задачах же интерполяции интервал варьирования охватывает всю описываемую область.
Выбор интервалов варьирования – задача трудная, так как она связана с неформализованным этапом планирования эксперимента. Возникает вопрос, какая априорная информация может быть полезна на данном этапе? Это – сведения о точности, с которой экспериментатор фиксирует значения факторов, о кривизне поверхности отклика и о диапазоне изменения параметра оптимизации. Обычно эта информация является ориентировочной (в некоторых случаях она может оказаться просто ошибочной), но это единственная разумная основа, на которой можно начинать планировать эксперимент. В ходе эксперимента ее часто приходится корректировать.
Точность фиксирования факторов определяется точностью приборов и стабильностью уровня в ходе опыта. Для упрощения схемы принятия решений мы введем приближенную классификацию, полагая, что есть низкая, средняя и высокая точности. Можно, например, считать, что поддержание температуры в реакторе с погрешностью не более 1% соответствует высокой, не более 5% – средней, а более 10% – низкой точности.
Источником сведений о кривизне поверхности отклика могут служить уже упоминавшиеся графики однофакторных зависимостей, а также теоретические соображения. Из графиков сведения о кривизне можно получить визуально. Некоторое представление о кривизне дает анализ табличных данных, так как наличию кривизны соответствует непропорциональное изменение параметра оптимизации при равномерном изменении фактора. Мы будем различать три случая: функция отклика линейна, функция отклика существенно нелинейна и информация о кривизне отсутствует.
Наконец, полезно знать, в каких диапазонах меняются значения параметра оптимизации в разных точках факторного пространства. Если имеются результаты некоторого множества опытов, то всегда можно найти наибольшее или наименьшее значения параметра оптимизации. Разность менаду этими значениями будем называть диапазоном изменения параметра оптимизации для данного множества опытов. Условимся различать широкий и узкий диапазоны. Диапазон будет узким, если он не существенно отличается от разброса значений параметра оптимизации в повторных опытах (этот разброс определяет ошибку опыта). В противном случае будем считать диапазон широким. Учтем также случай, когда информация отсутствует. Итак, для принятия решений используется априорная информация о точности фиксирования факторов, кривизне поверхности отклика и диапазоне изменения параметра оптимизации. Каждое сочетание градаций перечисленных признаков определяет ситуацию, в которой нужно принимать решение. При принятых градациях возможно З3 = 27 различных ситуаций. Они представлены на рис. 3, 4, 5 в виде кружочков, цифры в которых соответствуют порядковым номерам ситуаций.
Теперь мы приблизились к принятию решения о выборе интервалов варьирования. Для интервалов также введем градацию. Будем рассматривать широкий, средний и узкий интервалы варьирования, а также случай, когда трудно принять однозначное решение. Размер интервала варьирования составляет некоторую долю от области определения фактора. Можно, например, условиться о следующем: если интервал составляет не более 10% от области определения, считать его узким, не более 30% – средним, и в остальных случаях – широким. Это, конечно, весьма условно, и в каждой конкретной задаче приходится специально определять эти понятия, которые зависят не только от размера области определения, но и от характера поверхности отклика и от точности фиксирования факторов.
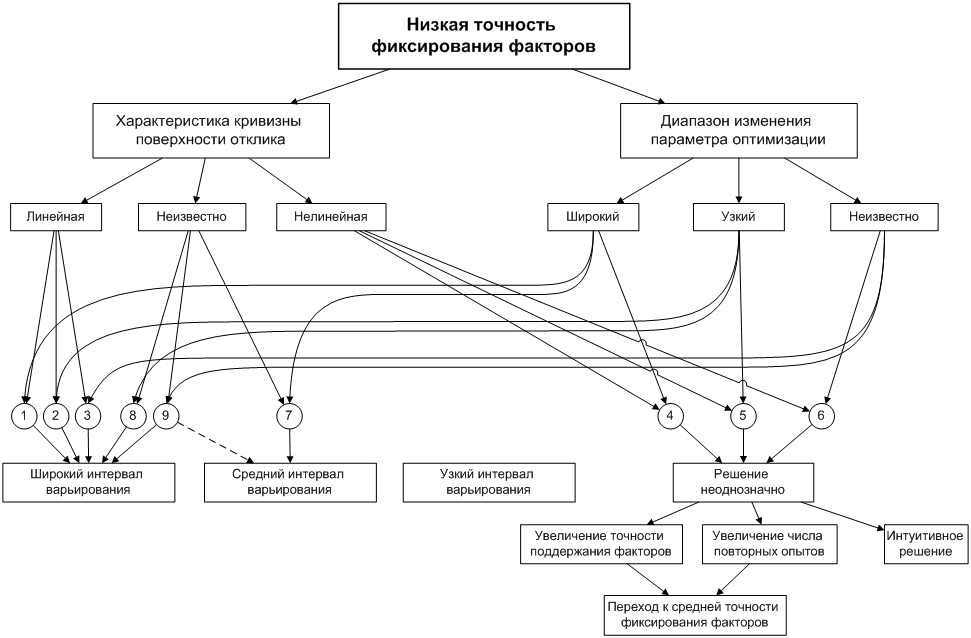
Перейдем к рассмотрению блок-схем принятия решений. На первой схеме (рис. 3) представлены девять ситуаций, имеющих место при низкой точности фиксирования факторов. При выборе решений учитываются информация о кривизне поверхности отклика и о диапазоне изменения параметра оптимизации. Типичное решение – широкий интервал варьирования, узкий интервал варьирования совершенно не используется, что вполне понятно при низкой точности.
Средний интервал варьирования в этой схеме выбирается дважды, причем в девятой ситуации как редко применяемая альтернатива. Здесь отсутствует информация об обоих признаках и выбор широкого интервала представляется более естественным.
Наибольшие трудности возникают, когда поверхность отклика нелинейна. Появляется противоречие между низкой точностью фиксирования факторов и кривизной. Первая требует расширения интервала, а вторая – сужения. Решение оказывается неоднозначным. Как поступить? Приходится рассматривать дополнительные рекомендации (см. блок-схему). Прежде всего, нужно выяснить, нельзя ли увеличить точность эксперимента либо за счет инженерных решений, либо за счет увеличения числа повторных опытов. Если это возможно, то решения принимаются на основе блок-схемы (рис. 4) для средней точности фиксирования факторов. Если это невозможно, то для принятия решения нет достаточных оснований и оно становится интуитивным.
Эта блок-схема, как и последующие, служит весьма грубым приближением к действительности. На практике учитывается ещё масса обстоятельств. Например, решения, принимаемые по каждому фактору в отдельности, корректируются при рассмотрении совокупности факторов.
Рисунок 3
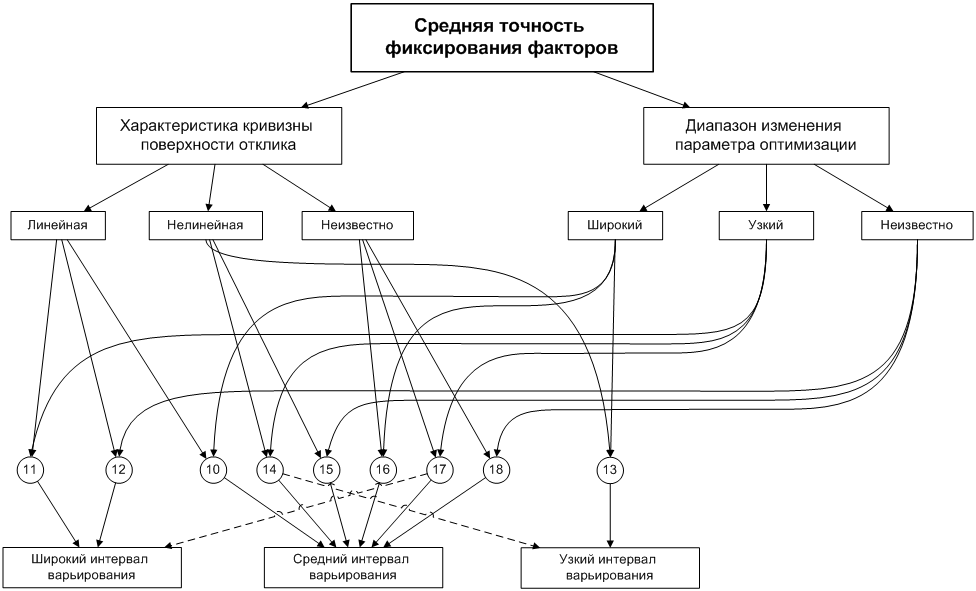
Рисунок 4
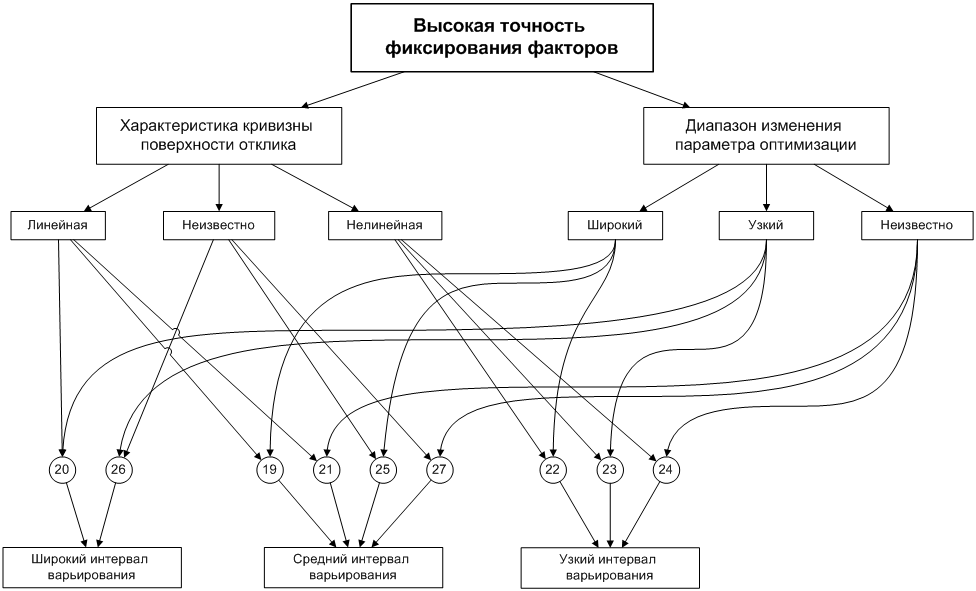
Рисунок 5
На рис. 4 изображена блок-схема для случая средней точности фиксирования фактора. Характерен выбор среднего интервала варьирования. Лишь в случае нелинейной поверхности и широкого диапазона рекомендуется узкий интервал варьирования. При сочетаниях линейной поверхности с узким диапазоном и отсутствием информации о диапазоне выбирается широкий интервал варьирования. Пунктиром, как и выше, показаны редко применяемые альтернативы.
Наконец, на рис. 5 построена блок-схема для случая высокой точности фиксирования фактора. Сочетание высокой точности с нелинейностью поверхности всегда приводит к выбору узкого интервала. Довольно часто выбирается средний интервал и лишь в двух случаях широкий. В обеих последних блок-схемах отсутствуют неоднозначные решения.