Оглавление

Ограничения

Основные определения

Объект исследования

Параметр оптимизации

Виды параметров оптимизации

Требования к параметру оптимизации

Факторы

Определение фактора

Требования, предъявляемые к факторам при планировании эксперимента

Требования к совокупности факторов

Выбор модели

Шаговый принцип

Как выбрать модель?

Полиномиальные модели

Полный факторный эксперимент

Принятие решений перед планированием эксперимента

Выбор основного уровня

Выбор интервалов варьирования.

Полный факторный эксперимент

Свойства полного факторного эксперимента типа 2^k

Полный факторный эксперимент и математическая модель

Дробный факторный эксперимент

Минимизация числа опытов

Дробная реплика

Выбор полуреплик. Генерирующие соотношения и определяющие контрасты..

Выбор 1/4-реплик. Обобщающий определяющий контраст.

Реплики большой дробности

Проведение эксперимента

Ошибки параллельных опытов

Дисперсия параметра оптимизации

Проверка однородности дисперсий

Рандомизация

Разбиение матрицы типа 2^k на блоки

Обработка результатов эксперимента

Метод наименьших квадратов

Регрессионный анализ

Проверка адекватности модели

Проверка значимости коэффициентов

Принятие решений после построения модели

Интерпретация результатов

Принятие решений после построения модели процесса

Построение интерполяционной формулы, линейная модель неадекватна

Крутое восхождение по поверхности отклика

Движение по градиенту

Расчет крутого восхождения

Реализация мысленных опытов

Принятие решений после крутого восхождения

Крутое восхождение эффективно

Крутое восхождение неэффективно

Дополнительные материалы

Глава 1

Глава 2

Глава 3

Глава 4

 

Проведение эксперимента

 

Познакомимся с вычислением ошибки опыта, или, как ее часто называют, ошибки воспроизводимости.

Ошибки параллельных опытов

Каждый эксперимент содержит элемент неопределен­ности вследствие ограниченности экспериментального ма­териала. Постановка повторных (или параллельных) опытов не дает полностью совпадающих результатов, потому что всегда существует ошибка опыта (ошибка воспроиз­водимости). Эту ошибку и нужно оценить по параллель­ным опытам. Для этого опыт воспроизводится по возмож­ности в одинаковых условиях несколько раз и затем бе­рется среднее арифметическое всех результатов. Среднее арифметическое  равно сумме всех п отдельных резуль­татов, деленной на количество параллельных опытов п

.

Отклонение результата любого опыта от среднего арифметического можно представить как разность  где  – результат отдельного опыта. Наличие откло­нения свидетельствует об изменчивости, вариации значе­ний повторных опытов. Для измерения этой изменчи­вости чаще всего используют дисперсию. Диспер­сией называется среднее значение квадрата отклонений величины от ее среднего значения. Дисперсия обозна­чается s² и выражается формулой

.

где (n – 1) – число степеней свободы, равное количе­ству опытов минус единица. Одна степень свободы исполь­зована для вычисления среднего.

Корень квадратный из дисперсии, взятый с положи­тельным знаком, называется средним квадратическим от­клонением, стандартом или квадратичной ошибкой

Стандарт имеет размерность той величины, для кото­рой он вычислен. Дисперсия и стандарт – это меры рассеяния, изменчивости. Чем больше дисперсия и стан­дарт, тем больше рассеяны значения параллельных опы­тов около среднего значения.

Ошибка опыта являемся суммарной величиной, результатом многих ошибок: ошибок измерений факторов, ошибок измерений параметра оптимизации и др. Каждую из этих ошибок можно, в свою очередь, разделить на состав­ляющие.

Вопрос о классификации ошибок довольно сложный и вызывает много дискуссий. В качестве примера одной из возможных схем классификации мы приведем схему из книги Ю. В. Кельница «Теория ошибок измере­ний» (М., изд-во «Недра», 1967).

 

 

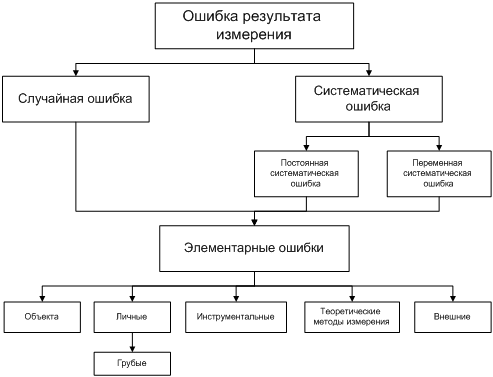
Все ошибки принято разделять на два класса: система­тические и случайные.

Систематические ошибки порождаются причинами, действующими регулярно, в определенном направлении. Чаще всего эти ошибки можно изучить и определить количественно.

Систематические ошибки находят, калибруя измери­тельные приборы и сопоставляя опытные данные с изме­няющимися внешними условиями (например, при градуи­ровке термопары по реперным точкам, при сравнении с эта­лонным прибором).

Если систематические ошибки вызываются внешними условиями (переменной температуры, сырья и т. д.), следу­ет компенсировать их влияние. Как это делать, будет показано ниже.

Случайными ошибками называются те, которые появ­ляются нерегулярно, причины возникновения которых неизвестны и которые невозможно учесть заранее.

Систематические и случайные ошибки состоят из мно­жества элементарных ошибок. Для того, чтобы исключать инструментальные ошибки, следует проверять приборы перед опытом, иногда в течение опыта и обязательно после опыта. Ошибки при проведении самого опыта возникают вследствие неравномерного нагрева реакционной среды, раз­ного способа перемешивания и т.п. При повторении опытов такие ошибки могут вызвать большой разброс эксперимен­тальных результатов.

Очень важно исключить из экспе­риментальных данных грубые ошибки, так называемый брак при повторных опытах. Для отброса оши­бочных опытов существуют правила. Для определения брака используют, например, кри­терий Стьюдента

.

Значение t берут из таблицы t-распределения Стьюдента. Опыт считается бракованным, если эксперименталь­ное значение критерия t по модулю больше табличного значения.

Дисперсия параметра оптимизации

 

Дисперсия всего эксперимента получается в результате усреднения дисперсий всех опытов. По терми­нологии, принятой в планировании эксперимента, речь идет о подсчете дисперсии параметра оптимизации  или, что то же самое, дисперсии воспроизводимости эксперимента

При подсчете дисперсии параметра оптимизации квад­рат разности между значением y_q в каждом опыте и средним значением из n повторных наблюдений y нужно просумми­ровать по числу опытов в матрице N, а затем разделить на N(n - 1):

,

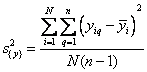Где i = 1, 2, …, N;      q = 1, 2, …, n.

 

Такой формулой можно пользоваться в случаях, когда число повторных опытов одинаково во всей матрице.

Дисперсию воспроизводимости проще всего рассчиты­вать, когда соблюдается равенство числа повторных опы­тов во всех экспериментальных точках. На практике весь­ма часто приходится сталкиваться со случаями, когда число повторных опытов различно. Это происходит вследствие отброса грубых наблюдений, неуверенности экспе­риментатора в правильности некоторых результатов (в таких случаях возникает желание еще и еще раз повторить опыт) и т.п.

Тогда при усреднении дисперсий приходится пользо­ваться средним взвешенным значением дисперсий, взятым с учетом числа степеней свободы

,

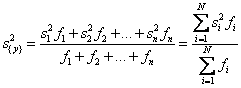где

– дисперсия i-го опыта;

 – число степеней свободы i-м опыте, равное числу параллельных опытов n_i минус 1.

Число степеней свободы средней дисперсии принима­ется равным сумме чисел степеней свободы дисперсий, из которых она вычислена.

Случай с неравным числом наблюдений, который мы рассмотрели выше, связан с нарушением ортогональности матрицы. Поэтому здесь нельзя использовать расчетные формулы для коэффициентов, приведенные ранее. Этот вопрос будет рассмотрен ниже.

Экспериментатору не следует забывать о про­верке однородности дисперсий, неоднородные дисперсии усреднять нельзя. Прежде чем пользоваться приведёнными выше формулами, нужно убедиться в однородности суммируемых дисперсий.

Проверка однородности дисперсий

 

Проверка однородности дисперсий производится с помощью различных статистических критериев. Простей­шим из них является критерий Фишера, предназначенный для сравнения двух дисперсий. Критерий Фишера (F-критерий) представляет собою отношение большей дисперсии к меньшей. Полученная величина сравнивается с таблич­ной величиной F-критерия.

Если полученное значение дисперсионного отно­шения больше приведенного в таблице для соответствую­щих степеней свободы и выбранного уровня значимости, это означает, что дисперсии значимо отличаются друг от друга, т. е. что они неоднородны.

Если сравниваемое количество дисперсий больше двух и одна дисперсия значительно превышает остальные, можно воспользоваться критерием Кохрена. Этот критерий пригоден для случаев, когда во всех точках имеется одина­ковое число повторных опытов. При этом подсчитывается дисперсия в каждой горизонтальной строке матрицы

,

а затем из всех дисперсий находится наибольшая  ко­торая делится на сумму всех дисперсий. Критерий Кохрена – это отношение максимальной дисперсии к сумме всех дисперсий

.

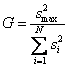Гипотеза об однородности дисперсий подтверждается, если экспериментальное значение критерия Кохрена не превы­шает табличного значения. Тогда можно усреднять дис­персии и пользоваться формулой

.

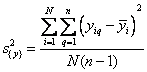Если возникает предположение о наличии неодно­родности дисперсий для случая, когда число повторных опытов неодина­ково во всех точках, можно воспользоваться критерием Бартлета. По уже знакомой формуле подсчитывается дисперсия воспроизводимости

.

Далее находится величина

,

где

.

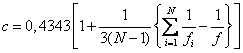Здесь число степеней свободы равно N–1, где N – число сравниваемых дисперсий. При планировании экспе­римента типа 2^k это число равно числу опытов в матрице.

Бартлет показал, что величина  приближенно подчиняется  – распределению с (N–1) степенями свободы. Значимость критерия Бартлета проверяется обычным способом.

Критерий Бартлета базируется на нормальном распре­делении. Если имеются отклонения от нормального распре­деления, то проверка неоднородности дисперсий может привести к ошибочным результатам.

Можно предложить использование F-критерия даже в тех случаях, когда число дисперсий больше двух. Делается это следующим образом. Из всех дисперсий выделяются наибольшая и наименьшая. По F-критерию производится проверка, значимо ли они различаются между собой. Ясно, что если наибольшая и наименьшая дисперсии не отличаются значимо, то диспер­сии, имеющие промежуточные значения, также не могут значимо отличаться друг от друга. Тогда всю группу дис­персий можно считать принадлежащей к единой совокуп­ности. В таких случаях нет надобности применять кри­терий Бартлета.

Рандомизация

 

Чтобы исключить влияние систематических ошибок, вызванных внешними условиями (переменой температуры, сырья, лаборанта и т. д.), рекомендуется случайная пос­ледовательность при постановке опытов, запланированных матрицей. Опыты необходимо рандомизировать во времени. Термин «рандомизация» происходит от английского слова random – случайный.

Разбиение матрицы типа 2^k на блоки

 

Если экспериментатор располагает сведениями о пред­стоящих изменениях внешней среды, сырья, аппаратуры и т. п., то целесообразно планировать эксперимент таким образом, чтобы эффект влияния внешних условий был сме­шан с определенным взаимодействием, которое не жалко потерять. Так, при наличии двух партий сырья матрицу 2³ можно разбить на два блока таким образом, чтобы эффект сырья сказался на величине трехфакторного взаимодейст­вия. Тогда все линейные коэффициенты и парные взаимо­действия будут освобождены от влияния неоднородности сырья.

 

 

В этой матрице при составлении блока 1 отобраны все строки, для которых , а при составления бло­ка 2 – все строки, для которых . Различие в сырье можно рассматривать как новый фактор . Тогда матрица 2³, разбитая на два блока, представляет собой полуреплику 2^4-1 с определяющим контрастом .

,                 ;

,                ;

,               ;

,                  ;

,                 ;

,              ;

,              ;

,                ;

Эффект сырья отразился на подсчете свободного члена b₀ и эффекта взаимодействия второго порядка b₁₂₃.

Аналогично можно разбить на два блока любой экспе­римент типа 2³. Главное – правильно выбрать взаимодей­ствие, которым можно безболезненно пожертвовать. При отсутствии априорных сведений выбирают взаимодействие самого высокого порядка: x₁x₂x₃ для 2³, x₁x₂x₃х₄ для 2⁴, x₁x₂x₃x₄x₅ 2⁵ и т. д. Но если экспериментатору известно, что одно из парных взаимодействий лишено, например, физико-химического смысла, то можно пожертвовать парным взаимодействием.

Матрицу типа 2^k можно разбить на количество блоков 2ⁿ (n – степень двойки) при . Так, матрица 2³ разбивается на два блока по четыре опыта в каждом и на четыре блока по два опыта в каждом. Матрица 2⁴ – на два блока по 8 опытов в каждом, на четыре блока по четыре опыта и на восемь блоков по два опыта и т.д.